Game Trees and Reversi
Many popular games such as Chess, Go, and Checkers share the fact that they can be boiled down into a game of throwing sticks into a fire commonly known as the game of Nim. This abstraction often takes the form of a tree with each node representing a possible board outcome and each sub-node to a given node representing a reachable board state from the current one. In the case of Chess and Go these trees become too complex to accurately and efficiently model. A 4x4 variant of Reversi, on the otherhand, has a much smaller tree. As a result it is a great starting point for understanding the stuctures that these types of games can create as well as how an AI can be developed to play these games.
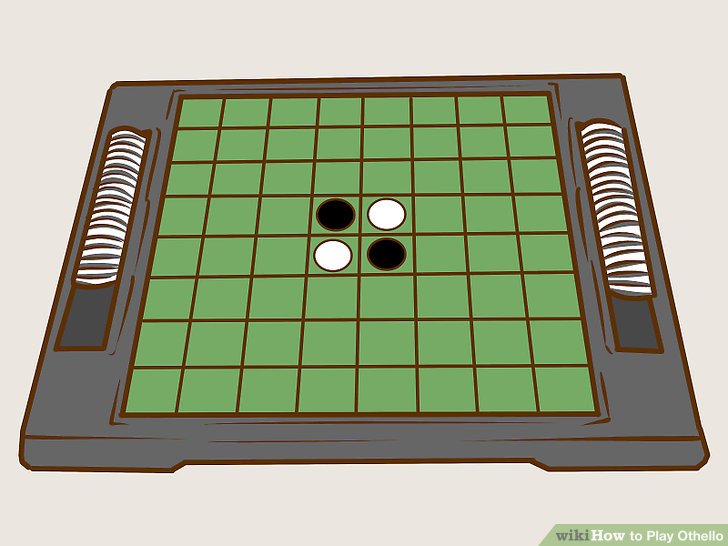
Reversi is a game played between two players, dark and light. We will have a board that is 4x4 in order to reduce the size of the game tree. The game starts with four tiles in the center of the board as shown above. The dark player will play first. To place a valid move, a player must place a tile such that a contiguous set of opposing pieces lies directly between two of the current players pieces. This placement will then cause the opposing tiles in between to change to the current players color. If a player has no available moves, priority will pass to the opposing player. If neither player has any available moves, the game is over and the number of tiles are scored. The winner is the player with more tiles of their color.
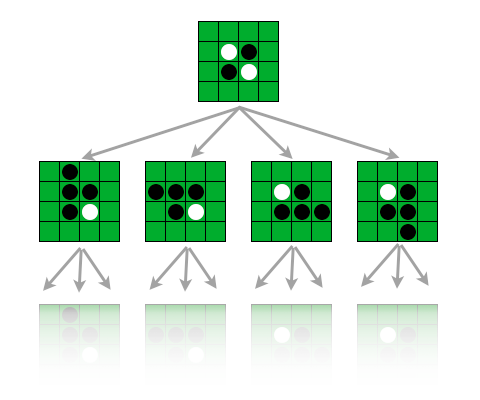
For the AI we will first construct a game tree for Reversi. In the above example we have a tree starting from the beggining of the game. A path in the tree will then correspond to a valid game played. At the bottom of the tree will be board states where no valid move can be made. In these positions the game is determined to be over. Each terminal board state will be assigned a score. If player two has more pieces the score will be negative one. If there is a tie, a score of one will be given. Finally, if player one wins, a score based on the number of player one’s tiles minus player twos will be the score. We can formulate this code as follows.
public int getScore() {
// Returns current value of board
int score = 0;
for(int i = 0; i < board.length; i++) {
if(board[i] == '1') {
score++;
} else if(board[i] == '2') {
score--;
}
}
if(score < 0) return -1;
return Math.min(1, score);
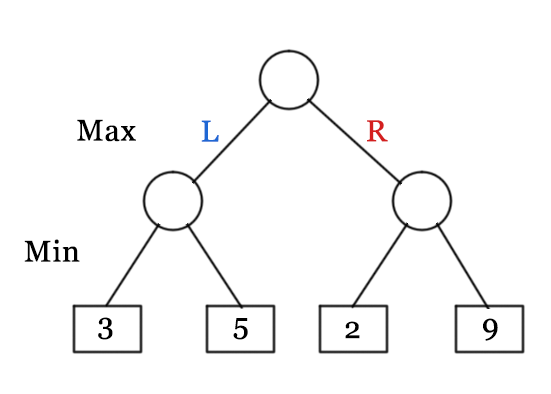
}We can determine the theoretical value of any board state through the Minimax algorithm. This will involve determining the outcome in the case of both players playing perfectly. In the algorithm Max will play first, and Min will play second. Max will always try to maximize their score while Min will always try to minimize theirs. Taking the bottom as an example, the bottom left node will have a value of three. This is because min will always take the minimum of all reachable states. The bottom right node will be two as that is the minimum between two and nine. The top node will then be the value three as max will choose the maximum between two and three. Using this procedure it is possible to construct a game tree where each possible board state has a value. Once the tree has been constructed all our AI will need to do is pick the optimal board state using this lookup table. One issue with this idea, however, is in the overall Complexity of the tree. In our case there are at most twelve turns. For each tile except for the center four tiles, it can have three final states. A dark or light tile is placed on it, or no tile is placed on it. For the center four tiles they are either light or dark. As a result we can put an upperbound on the size of the tree quite easilly by three to the twelve multiplied by sixteen. That is approximately 8 and a half million possible board states! As a result we are motivated to consider ways of reducing the parts of the tree actually looked at.
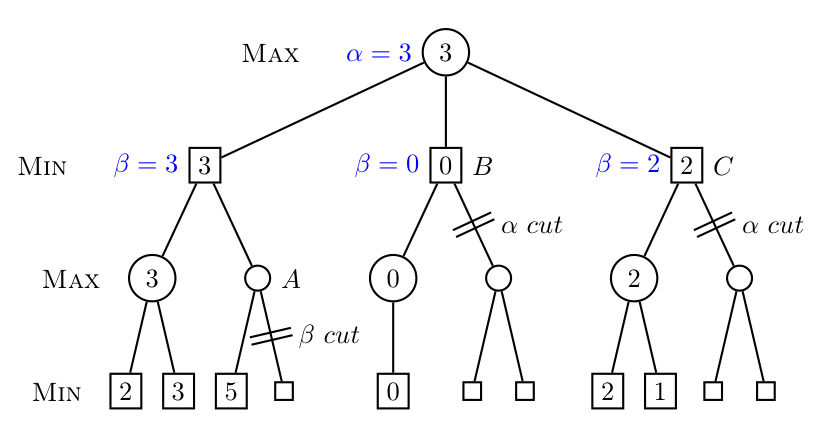
One solution to this issue is through an algorithm called Alpha-beta pruning. The idea behind this algorithm is to only look at sections of the tree that can alter current decisions. The algorithm does this by assigning an alpha and beta value to each board state in the tree. Initially these values are set to infinity for beta and negative infinity for alpha. For a board state in the tree where max makes a decision, the alpha value obtained is used in updating the parents beta value. On nodes where min makes a decision the beta value obtained determines the alpha value for its parent. Determining the alpha value is done by iterating through each child and updating the node’s alpha value based on the larger of the current alpha value and the beta value of the child node. Additionally, beta values from max parent nodes are passed down as alpha values of child nodes. The opposite is done for min nodes. As an example to better understand this algorithm we can look at the provided tree below. Starting down the left branch, we obtain a max value of three updating alpha for that node to be three. This value is then passed onto make beta of the parent node three as well. Going down the other branch we reach node A. Here after looking at the first node alpha has a value of five. The alpha value for node A will now be five and the beta value is three. Since beta is less than alpha we do not continue looking at the rest of that branch. This intuitively makes sense as max will always choose three if min chooses the left path and max will always choose at least five if min goes down the right path and chooses node A. As a result min will choose three as there is no possible values that could make node A a better decision.
When writing the code for this. We will create two methods. The first will be for determining the value assigned to a board state by max, and the second will be for determining the value min assigns to a board position. We will only look at max for this post as min will be the same but with alpha and beta switched as well as swapping minimum and maximum. If the board state is terminal the score is simply the score for the board state. If either max or min cannot move, then the algorithm will check for the value the opposing side assigns to the node. If max can play, the algorithm will look at each child node and update its alpha value until the alpha value becomes greater than its beta value or it has looked at all potential moves. At this point it will return the value for that node. This value will then get stored in the parents beta value.
public static int count = 0;
private static int max_value_with_pruning(State curr_state, int alpha, int beta) {
// Gets the max value possible at a node
int score = 0;
if(curr_state.isTerminal()) {
return curr_state.getScore();
}
State[] successors = curr_state.getSuccessors('1');
if(successors.length == 0) {
if(curr_state.getSuccessors('2').length != 0) {
return min_value_with_pruning(curr_state, alpha, beta);
} else {
return curr_state.getScore();
}
}
for(int i = 0; i < successors.length; i++) {
score = min_value_with_pruning(successors[i], alpha, beta);
alpha = Math.max(score, alpha);
if(alpha >= beta) {
return beta;
}
}
return alpha;
}The code for determining the value min obtains at a node as well as any additional code used for this game can be found at the repository. Additionally if you have a working version of Java 8, you can try out the game by downloading it here.